In the world of mathematics, two things always hold true: firstly, some of the most stubborn and complex problems often have surprisingly real-world applications; and secondly, for people who spend all their time actually in that real world, those problems can seem… well, pretty silly.
Take, for example, the “sofa problem”: a conundrum that has both stumped mathematicians for decades, and also been “solved” by just about anybody who’s ever moved house in their life. It’s a question of how to move a curved sofa around a 90-degree corner – yes, just like in that one episode of Friends you’re all now quoting.
The math of moving
Technically, the sofa problem is this: What is the region of largest area which can be moved around a right-angled corner in a corridor of width one? It was first formally stated in 1966 by the Austrian-Canadian mathematician Leo Moser – though it had been a topic of conversation around the mathematical water coolers for many years before that – and until now, never conclusively solved.
Now, you’ll notice that there’s no mention of the eponymous settee in this formulation, and indeed the first piece of “furniture” suggested as a solution was actually a “piano”. Nevertheless, the “sofa” terminology soon took off, mostly because – well, look at it:
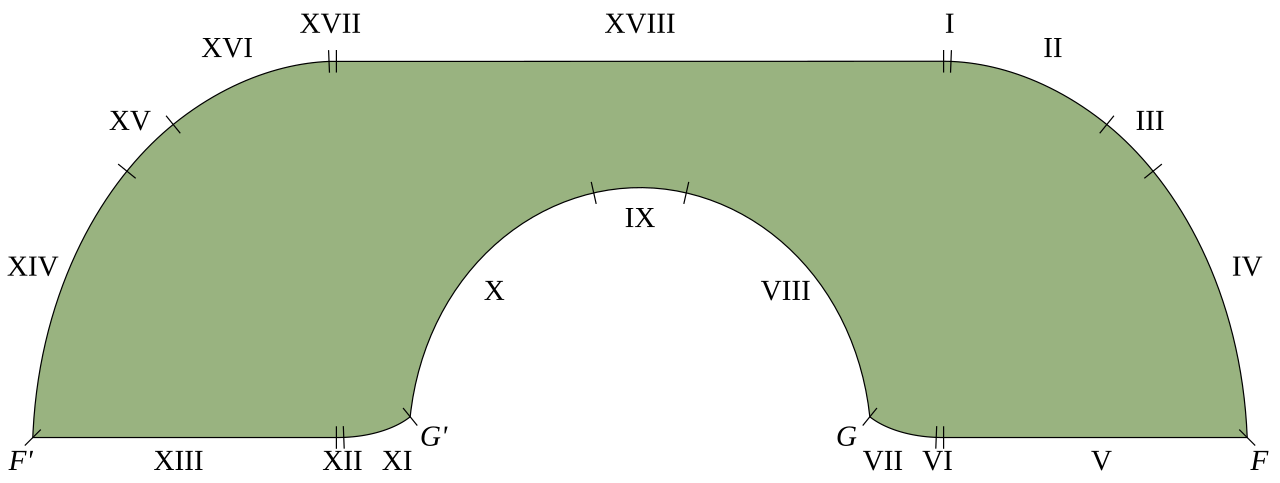
The Gerver sofa, showing each of the 18 segments making up its boundary.
It was the determination of a lower bound that gave rise to the iconic sofa shape: in a 1968 treatise named, we kid you not, On the enfeeblement of mathematical skills by ‘Modern Mathematics’ and by similar soft intellectual trash in schools and universities, John Hammersley showed with some relatively simple calculus that this shape gave an area of (π/2) + (2/π) – roughly 2.2074.
In fact, he went further. In the same paper, he proved that an upper bound on the area was given by 2√2 – roughly 2.8284. It had only been a couple of years, but the sofa problem was already on its way to a solution: the exact figure hadn’t been nailed down yet, but mathematicians knew it had to be between these two values. Surely it wouldn’t take much more work to find the true answer?
Fast forward 25 years, though, and Hammersley’s bounds were still the best we had. That was, until Rutgers mathematician Joseph Gerver stepped up to the plate, offering a sofa constructed from 18 analytically smooth connected curve sections. The “Gerver sofa”, as it became known, increased the lower bound to 2.2195.
It would be another quarter-century again before the range of possible solutions would be pared down even further: in 2018, mathematicians Yoav Kallus and Dan Romik used a computer-assisted proof to shave the upper bound down to 2.37.
It was a big improvement on Hammersley’s original bounds – but that exact solution was still evading capture.
Baek in the game
It would have been around the same time as Kallus and Romik were working on their solution that Jineon Baek, a postdoctoral researcher at Yonsei University in Seoul, Korea, first started thinking about the sofa problem. Now, seven years later, he reckons he’s cracked it in a proof that has yet to be peer-reviewed.
“I dedicated a lot of time to this, without any publication so far,” he told New Scientist. “The fact that now I can say to the world that I committed something valuable to this problem is validating.”
For a question so easily stated and imagined, Baek’s proof was no small undertaking. Spanning more than 100 pages, it does far more than simply brute force the problem or continuously shave off ever-smaller slices of area. Rather, it is, Romik told New Scientist, a “wonderful development”.
“I know I could never have done this,” Romik said. “I don’t have a feeling of regret, or like, how could I miss this, because it’s clear it’s just not the sort of thinking that I think I would have been able to. [Baek] was just coming at it from a completely different direction.”
Without getting into the nitty-gritty, the proof goes like this: first, Baek said that the optimal sofa, whatever it turned out to be, had to have three specific properties – it had to be monotone, balanced, and have a rotation angle π/2. Again, these are quite technical to define, but essentially it boils down to this: the “sofa” we’ve been using so far is pretty much the right shape already.
Secondly, Baek set about proving a condition on how this sofa would move around the corner – a small thing, but crucial for completing the final step: defining the upper bound for the area of this sofa, and then showing that it was equal to Gerver’s lower bound.
That’s right: after 32 years, it turns out Gerver was right all along.
“I am of course very happy about all of this,” Gerver told New Scientist. “I am 75 years old, and Baek can’t be more than 30. He has a lot more energy, stamina and surviving brain cells than I do, and I am glad that he picked up the baton. I am also very happy that I lived long enough to see him finish what I started.”
Put your feet up
So, is the sofa problem now complete? Well, technically, it remains to be seen. As with all mathematical proofs, it needs to be peer-reviewed for accuracy – a process that Baek is quietly hopeful for.
“I can’t say that I’m confident 100 per cent, because we are humans, we make errors,” he told New Scientist. “But still, I did my best to be as confident as I can.”
But if your hopes of solving the sofa problem yourself have been dashed by this news, take heart: since Baek defined his sofa so strictly, you can always choose a different shape for your own.
It might not make quite as good a sofa for your living room of course, but there’s really nothing stopping you from going… Baek to the drawing board, you might say.
The proof can be found on the ArXiv preprint server.













