For close to 40 years, a simple little hypothesis has been quietly sitting in a corner of graph theory, minding its own business. Known as the “bunkbed conjecture”, it always seemed kind of self-evidently true – sure, nobody could prove it, but it made sense – and certainly, nobody had ever found a counterexample.
Until now. In a surprise to pretty much everybody, a group of mathematicians announced a paper last month that they claim proves the conjecture is false. Currently published on the arXiv preprint server, and thus not yet peer-reviewed, the paper is nevertheless already making waves in the mathematical world – not only for the proof itself, but for what it says about math as an entire discipline.
The conjecture
First posited by the physicist Pieter Kasteleyn to a colleague in 1985, the bunkbed conjecture really has nothing to do with beds at all. Rather, it concerns graphs – and unless you’re a working mathematician, probably not the kind of graphs you’re thinking of right now.
“A graph consists of a bunch of vertices and a bunch of edges that connect the vertices,” explains Trefor Bazett, an Assistant Teaching Professor in the University of Victoria’s Mathematics and Statistics department, in a recent YouTube video about the proof.
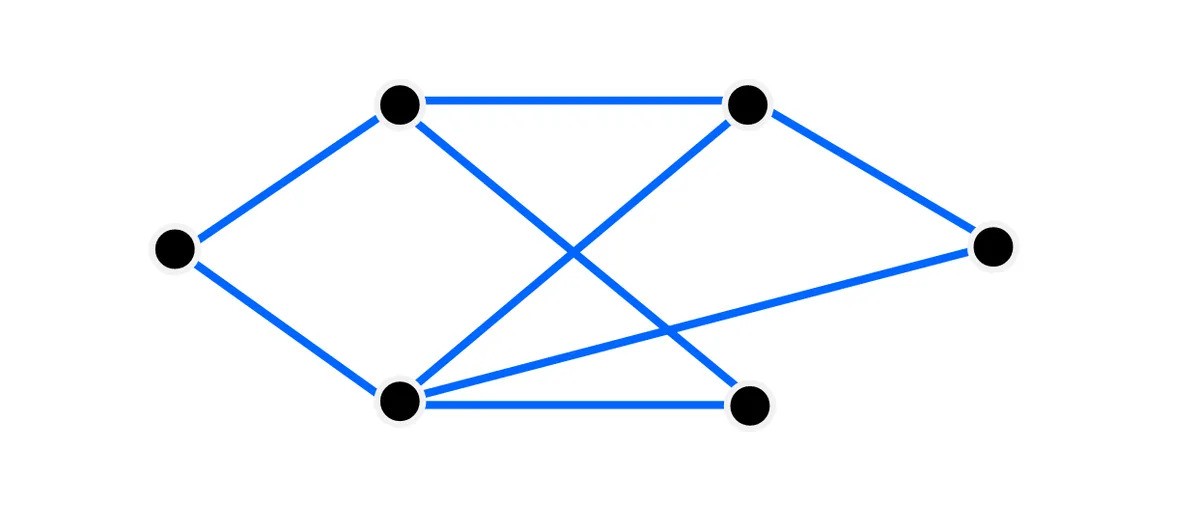
A graph with six vertices and eight edges.
Image credit: IFLScience
“You can imagine, perhaps, people in a social network,” he suggests, “and then the connection is whether or not you’re friends.”
Double this graph exactly, and you can create what’s known as a bunkbed graph: two identical graphs on top of each other, connected by “posts”. Look, once you see it in person, you’ll understand all the themed terminology.
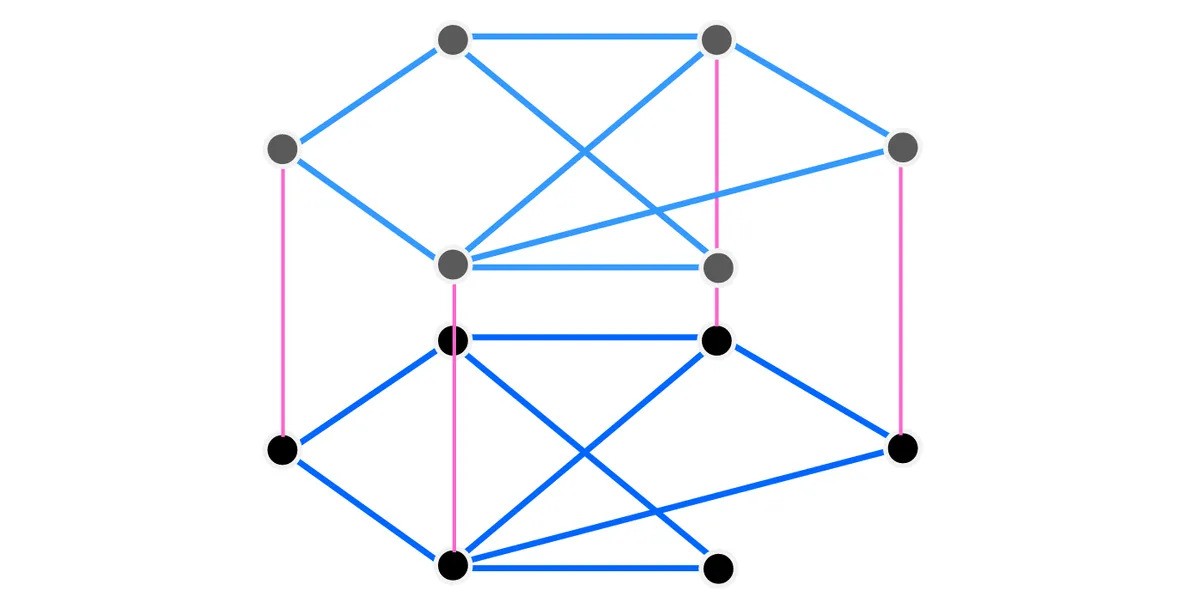
The same graph put in bunkbed formation. Those pink vertices are called the bedposts.
Image credit: IFLScience
So, we have our setup – our friendships between people, or locations on a map connected by streets, or whatever you’re imagining your graph to represent. Now we’re just going to think about how to move through the graph itself – so, say you want to get from point u to point v in our graph above, we have the following options:
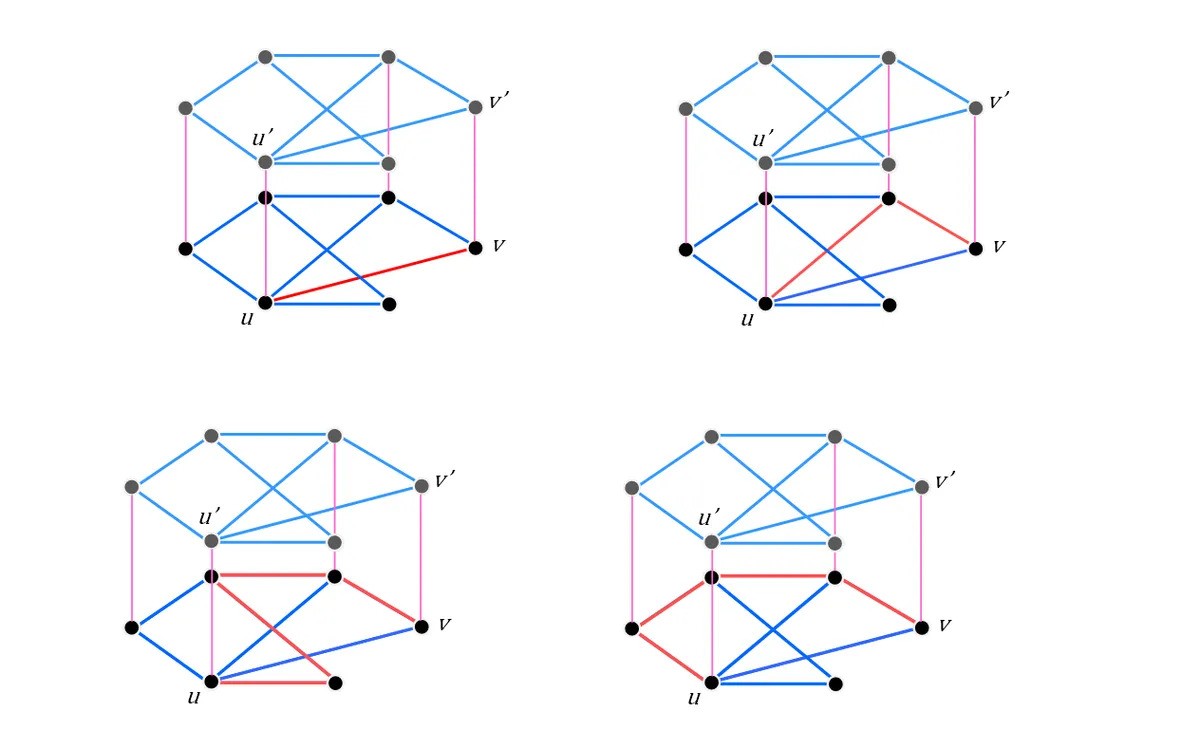
Four potential routes (not exhaustive!) from u to v highlighted in red.
Image credit: IFLScience
With us so far? Great, because this is where things get a bit more complicated. What we’re going to do now is delete some of the edges – lose friends; block up streets, whatever you like – and see how likely it is that we can still get from u to v afterward.
So, with all that background, we can now get to the statement of the bunkbed conjecture, which is this: P(u ↔ v) ≥ P(u ↔ v’).
“It says that the probability that I can get from u to v – that is, the probability that I can move along the base – is bigger or equal to the probability that I can start in the base and then get to v’ […] on the top bunk,” Bazett explained.
“The conjecture says that this is true for all connected graphs, and all subsets of bedposts, and all pairs u and v.”
Intuitively, it makes sense: surely, it’s going to be easier to reach an endpoint on the same level as your starting point than one that requires you to travel up a bedpost as well. Trying a few examples will only bolster that conviction – unless, that is, you’re willing to construct a graph with a few thousand vertices and edges.
The proof
Often, in math, disproving a hypothesis is easier than proving it. After all, to prove something, you have to show it’s true for every possible example, in all situations – to disprove it, you only have to find a single counterexample.
The problem with the bunkbed conjecture was – well, nobody was looking for that counterexample. “Why look for a counterexample if the conjecture is so obviously true?” wrote Igor Pak, a math professor at UCLA and one of the authors of the new paper, in a blog post on the breakthrough.
“Well, because you always should,” he countered. “For any conjecture. Especially if everyone else is so sure, as in completely absolutely sure without a doubt, that the conjecture is true.”
Now, it’s the 2020s; you know how math is done these days, and so did Pak. “We started with a myriad of computer experiments trying all small graphs,” he wrote. “When those failed, we tried to use AI and other computer assisted tools.”
Even still, no counterexamples seemed to be forthcoming – and the team started worrying that, even if one did turn up, it wouldn’t be enough to fully disprove the conjecture. The graphs being sampled by the neural networks were so large at that point that calculating the relevant probabilities exactly would be impossible, and so any proof would be at best something like 99.9999 percent certain to be correct.
But while “99.99 percent confidence […] may be a gold standard in nuclear physics,” Pak wrote, “math journals tend to prefer 100 percent correctness.”
“Most journals would refuse to even consider a ‘five sigma counterexample’,” he added.
So, rather than persevere with machine learning techniques that weren’t bearing fruit – and whose results may not be accepted even if it was successful – the team took a step back. And then, in June of this year, a paper hit the arXiv which changed everything.
“I found it in the evening, and I read it until 3 a.m.,” Nikita Gladkov, one of Pak’s graduate students and a co-author of the paper, told Quanta. “I was like, ‘Wow, this is crazy. Absolutely mind-boggling.’”
It wasn’t a proof of the bunkbed conjecture exactly, but it was close – a formulation of the statement which dealt with objects called hypergraphs, rather than graphs. The author, a postgraduate student at the University of Cambridge and accomplished googologist named Lawrence Hollom, had shown that in these objects, the bunkbed conjecture was… false.
Hollom had presented his work as an attempt to generalize the bunkbed conjecture – or, as it turned out, to show that it couldn’t be generalized. In the end, though, it was his paper that would inspire the proof of the original conjecture.
By converting Hollom’s hypergraph, the team created a graph that could potentially disprove the bunkbed conjecture. It was absolutely monstrous – 7,222 vertices, connected by 14,442 edges – and the difference in the relevant probabilities was minute: “astronomically small,” Pak wrote, “on the order of -10-6500.”
“But it’s negative, which is all we need,” he added. The conjecture was officially false.
The upshot
So, what does this mean, other than the obvious? Well, there are some disappointments, particularly for applied mathematicians and physicists: had the bunkbed conjecture turned out to be true, it would have validated a widely believed assumption about how fluids travel through solids, and given a handhold to researchers investigating the physics of percolation.
But more than that, there are the moral impacts of the breakthrough. Should future mathematicians be more willing to accept probabilistic proofs? Would they be as valid, or as complete?
“It’s a philosophical question,” Noga Alon, a math professor at Princeton, told Quanta. “How do we view proofs that are only true with high probability?”
“Maybe a probabilistic proof would give you less understanding or intuition of what’s really going on,” he said.
Finally, it’s a warning to mathematicians not to accept a conjecture just because they like it. “We have to be suspicious, even about things that intuitively look very likely to be true,” Alon said.
It’s a sentiment that Pak has long championed. “Some conjectures are motivated by substance,” he told Quanta, “and other conjectures are motivated by wishful thinking.”
The bunkbed conjecture, it seems, was the latter.
The paper, which is not yet peer-reviewed, can be found on the arXiv.













